반응형
Spanning Tree(신장트리)
그래프 내의 모든 정점을 포함하는 트리
- 모든 정점들이 연결되어 있어야하고, 사이클을 포함해서는 안된다.
- 그래프의 최소 연결 부분 그래프이다.
- 최소연결 = 간선의 수가 가장 적다
- 그래프에 있는 n개의 정점(vertax)을 가지는 그래프의 최소 간선(edge) 수는 (n-1)개이고, (n-1)개의 간선으로 연결되 있으면 필연적으로 트리형태가 되므로 Spanning Tree가 되므로 즉, 그래프에서 일부 간선을 선택해서 만든 트리이다.
- 신장트리는 깊이 우선 탐색이나 너비 우선 탐색 을 이용하여 사용된 간선만 모으면 만들 수 있다.
- 하나의 그래프에 많은 신장 트리가 존재할 수 있다.
[시작 정점을 바꾸어 가면서 깊이 우선 탐색을 하여 만든 신장 트리 중 일부]

깊이우선 탐색알고리즘을 이용하여 만든 신장 트리 알고리즘
depth_first_search(v)
v를 방문되었다고 표시:
for all u <= (v에 인접한 정점) do
then (v, u)를 신장 트리 간선이라고 표시;
depth_first_search(u)Minimum Spanning Tree(MST)
최소비용 신장트리 또는 최소비용 스패닝 트리라고 불리며 사용된 간선들의 가중치 합이 최소인 Spanning Tree를 말한다.
- 간선의 가중치 합이 최소여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시(n-1)개의 간선만 사용해야 한다.
- 사이클이 포함되어서는 안된다.
사례
- 도로건설
- 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
- 전기 회로
- 단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제
- 통신
- 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
- 배관
- 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제
구현방법
1. Kruskal MST 알고리즘
탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것.
- MST가 최소비용의 간선으로 구성
- 사이클이 포함되지 않다는 것을 조건으로 각 단계에서 사이클을 이루지 않는 최소 비용간선을 선텍
- 탐욕적인 방법이란?
- 결정을 해야할 때마다 그 순간마다 가장 좋다고 생각되는 것을 해답으로 선택함으로써 최종적인 해답에 도달하는 것.
알고리즘 절차
- 그래프의 e개의 간선들의 가중치를 오름차순으로 정렬한다.
- 정렬된 간선들의 리스트에서 사이클을 형성하지 않은 간선을 찾는다.
- 가장 낮은 가중치를 먼저 선택
- 만약 사이클을 형성하면 그 간선은 제외된다.
- 현재의 최소 비용 신장 트리의 집합에 추가한다.
//입력 : 가중치 그래프 G = (V, E) n은 노드의 개수
//출력 : E_t, 최소 비용 신장트리를 이루는 간선들의 집합
kruskal(G)
E의 가중치를 오름차순으로 정렬
**E_t = (집합)**
count <- 0
k <- 0
while count < (n - 1) do
k <- k + 1
if (E_t and {e_k} 가 사이클을 포함하지 않으면
then E_t < = Et U {e_k};
count <- count + 1
return E_t;
알고리즘 구현 시 주의사항
- 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지를 체크해야 한다.
- 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결할 때 사이클이 형성된다.
- 즉, 추가할 새로운 간선의 양끝 정점이 같은 집합에 속해 있으면(간선을 추가하였을 경우) 사이클이 형성된다.
사이클 생성 여부를 확인하는 방법
- 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지를 먼저 검사해야 한다.
- union-find 알고리즘 이용하면 사이클 생성여부를 확인할 수 있다.
- union(x,y) 연산 : 원소 x와 y가 속해 있는 집합을 입력 받아 2개의 집합의 합집합을 만든다.
- find(x) 연산 : 원소 x가 속해 있는 집합을 반환
package com.coding.exam;
import java.util.Arrays;
import java.util.Comparator;
public class KruskalAlgorithm {
public static void main(String[] args) {
Solution sol = new Solution();
int result = sol.kruskal(4, new int[][] {
{0,1,1},{0,2,2},{1,2,5},{1,3,1},{2,3,8}
});
System.out.println(result);
}
private static class Solution {
private int[] parent; //부모노드
private int[] rank; //각 집합의 크기
public int kruskal(int n, int[][] costs) {
init(n);
//가중치 값 작은 순으로 정렬
Arrays.sort(costs, Comparator.comparingInt(o -> o[2]));
int cost = 0;
int edges = 0;
//간선수 n -1
for (int[] edge : costs) {
if (edges == n - 1) {
break;
}
//서로 속한 집합이 다르면
if (find(edge[0]) != find(edge[1])) {
unionByRank(edge[0], edge[1]); //두 집합을 합친다.
cost += edge[2];
edges++;
}
}
System.out.println(Arrays.toString(rank));
return cost;
}
/**
* 초기화
* @param n
*/
private void init(int n) {
this.parent = new int[n];
this.rank = new int[n];
for (int i = 0; i < n; i++) {
this.parent[i] = i;
}
}
private int find(int x) {
if (parent[x] == x) {
return x;
}
//경로 압축
return parent[x] = find(parent[x]);
}
private void union(int x, int y) {
int root1 = find(x);
int root2 = find(y);
if (root1 == root2) {
return;
}
if (root1 < root2) {
parent[root2] = root1;
} else {
parent[root1] = root2;
}
}
/**
* 두 트리를 합칠 때 높이가 더 낮은 트리를 높이가 높은 트리의 밑에 자손을 넣어주는 방식
* 메모리를 배로 사용하므로 공간복잡도가 늘어난다.
* @param x
* @param y
*/
private void unionByRank(int x, int y) {
int root1 = find(x);
int root2 = find(y);
if (root1 == root2) {
return;
}
if (rank[root1] > rank[root2]) {
parent[root2] = root1;
} else if (rank[root1] < rank[root2]) {
parent[root1] = root2;
} else { //rank[root1] == rank[root2]
parent[root1] = root2;
rank[root2]++;
}
}
}
}시간복잡도
- 간선들을 정렬하는 시간에 좌우
- e개를 퀵정렬과 같은 효율적인 알고리즘으로 정렬한다면 시간복잡도는 O(elog₂e)이 된다.
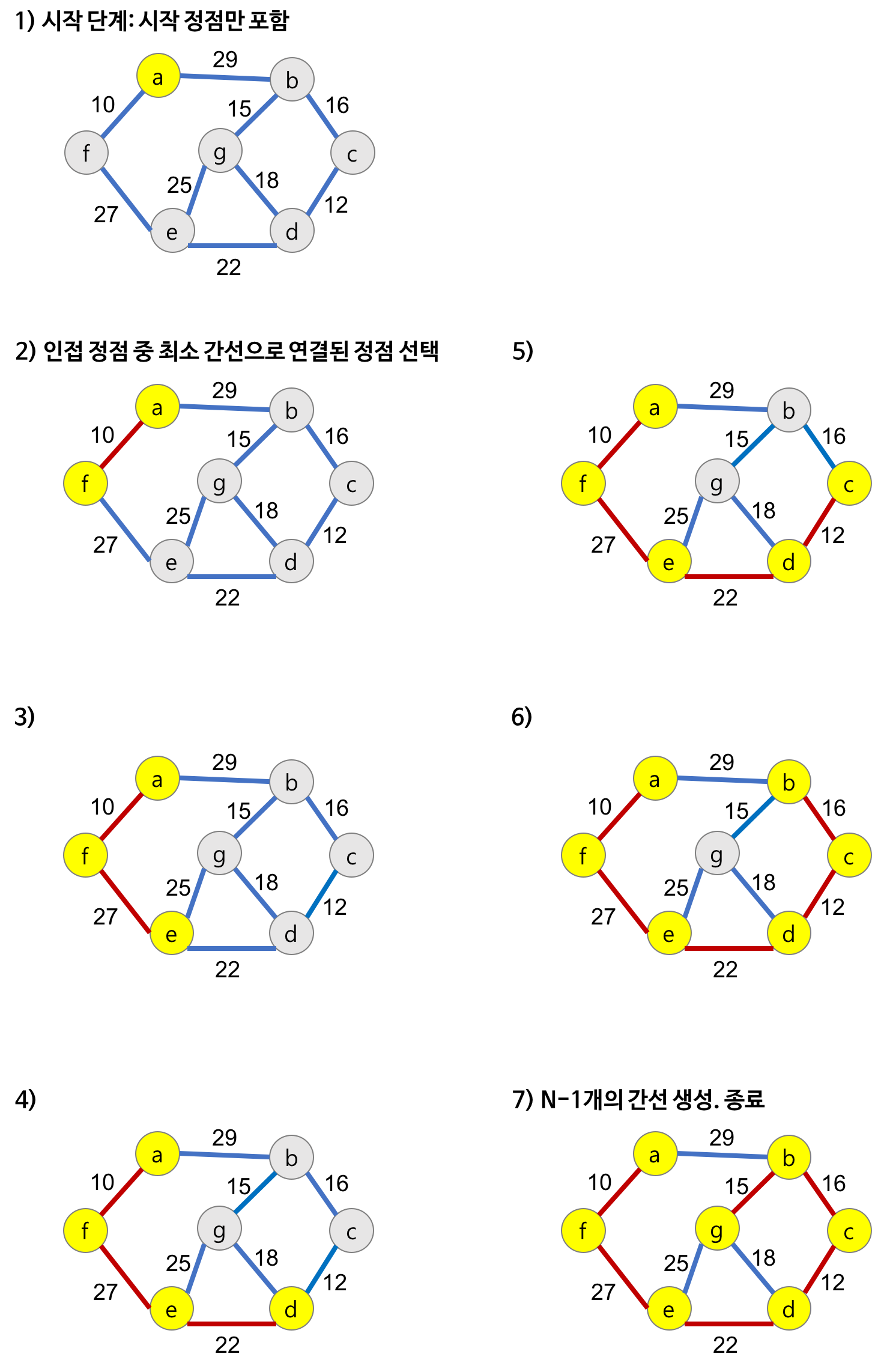
2. Prim MST 알고리즘
시작정점에서 정점을 추가하여 신장 트리 잡합을 단계적으로 확장해 나가는 방법
- 시작단계에서는 시작 정점만이 신장 트리 집합에 포함
- 앞 단계의 신장 트리 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장
- 인접한 정점들 중에서 가장 낮은 가중치의 간선과 연결된 정점을 선택하여 집합에 넣는 다는 것.
- 이 과정은 트리가 n-1개의 간선을 지날 때까지 반복
- 배열로 구현할 경우 시간 복잡도 o(n^2)
- 최소 힙으로 구현할 경우 시간 복잡도 O(Elog n)
//입력 : 네트워크 G=(V,E), s는 시작정점
//출력 : 최소 비용 신장트리를 이루는 정점들의 집합
Prims(G, s)
for each u ⊆ V do
dist[u] <- ∞
dist[s] <- 0
우선순위 큐 Q에 모든 정점을 삽입(우선순위는 dist[])
for i <- 0 to n-1 do
u <- delete_min(Q)
화면에 u 출력
for each v ⊆ (u의 인접 정점)
if ( v ⊆ Q and weight[u][v] < dist[v] )
then dist[v] <- weight[u][v]
초기상태 정점(vertex)는 서로 연결되어 있지 않은 상태로 정점과 연결된 간선을 하나씩 추가하면서 최소신장트리 집합을 만들어냄.
- 시작 정점을 정한 후 우선순위 큐에 넣는다.
- 우선순위 큐는 (정점, 가중치) 형식으로 저장
- 첫 시작은 (시작정점, 0)으로 넣는다.
- 우선순위 큐가 빌 때까지 반복 (n-1)
- 우선순위 큐에서 하나를 dequeue() [dequeue = 정점(v)]
- v가 이미 최소 신장 트리에 포함되어 있다면 1.을 수행, 그렇지 않으면 3. 진행
- v 와 연결된 간선을 모두 살핀다. 간선(w, cost)는 v와 정점 w 사이에 연결된 간선이며 cost의 가중치를 가지고 w를 방문하지 않으면 우선순위 큐에 추가
import java.util.*;
public class PrimAlgorithm {
public static void main(String[] args) {
Solution sol = new Solution();
int result = sol.solution(4, new int[][] {
{0,1,1},
{0,2,2},
{1,2,5},
{1,3,1},
{2,3,8}
});
System.out.println(result);
int result2 = sol.solution(5, new int[][] {
{1,3,3},
{1,4,8},
{4,5,9},
{1,2,10},
{2,5,14}
});
System.out.println(result2);
}
private static class Solution {
public int solution(int n, int[][] costs) {
List<List<Edge>> graph = new ArrayList<>();
for (int i = 0; i < n + 1; i++) {
graph.add(new ArrayList<>());
}
for (int[] cost : costs) {
graph.get(cost[0]).add(new Edge(cost[0], cost[2]));
graph.get(cost[0]).add(new Edge(cost[1], cost[2]));
}
return prim(graph, costs[0][0]);
}
public int prim(List<List<Edge>> graph, int start) {
Set<Integer> visited = new HashSet<>();
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(new Edge(start, 0));
int costs = 0;
while (!priorityQueue.isEmpty()) { //우선순위 큐가 빌 때까지 반복
Edge u = priorityQueue.poll();
if (visited.contains(u.vertex)) //방문했다면 건너뜀
continue;;
visited.add(u.vertex); // 방문하지 않았다면 vertex 방문했다고 표시
costs += u.cost; //가중치 증가
for (Edge edge : graph.get(u.vertex)) { //u.vertex 의 인접 정점 추가
if (!visited.contains(edge.vertex)) {
priorityQueue.add(edge);
}
}
}
return costs;
}
private static class Edge implements Comparable<Edge> {
int vertex;
int cost;
public Edge(int vertex, int cost) {
this.vertex = vertex;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(cost, o.cost);
}
@Override
public String toString() {
return "Edge{" +
"vertex=" + vertex +
", cost=" + cost +
'}';
}
}
}
}
Kruskal 알고리즘 Prim 알고리즘 차이
| Kruskal 알고리즘 | Prim 알고리즘 |
| 간선 선택을 기반으로 하는 알고리즘 | 정점 선택을 기반으로 하는 알고리즘 |
| 이전 단계에서 만들어진 신장 트리와 상관없이 최소 간선만을 선택하는 방법 | 이전 단계에서 만들어진 신장 트리를 확장하는 방식 |
참고 : c 언어로 쉽게 풀어 쓴 자료구조
반응형
'Algorithms' 카테고리의 다른 글
| 15. 그래프 최단경로(다익스트라, 벨만-포드) (4) | 2024.06.11 |
|---|