반응형
Tree(트리)
- 나무와 유사하게 비선형(데이터가 계층적 구조로 이루어짐) 구조로 이루어져 있는 자료구조
- 트리는 다른 자료구조보다 자료를 저장하거나 검색하는 방법이 간단하고 메모리를 효율적으로 사용할 수 있다.
구성
- 트리는 크게 Root(뿌리), Branch(가지),leaf(잎) 세 가지 요소로 이루어짐
- Root : 트리 구조에서 최상위에 존재하는 노드이다.
- Branch : Root Node or Sub Tree 와 leaf 사이에 있는 노드를 말한다(자식).
- Leaf(Terminal Node) : Branch Node의 맨 끝에 달려있는 노드로, 밑으로 또 다른 노드가 연결되어 있지 않은 노드를 말한다(Terminal(단말)노드).
- Node : 트리의 구성요소에 해당하는 요소를 말한다.
- Edge : 노드와 노드를 연결하는 연결선이다.
- Sub-Tree : 큰 트리(전체)에 속하는 작은 트리
- Level(Depth) : 루트노드에서 해당 노드까지 경로의 길이로 트리에서 각 층별로 숫자를 매김
- Height : 트리의 최고 레벨 (3)
- Length : 출발 노드에서 목적 노드까지 거쳐야하는 노드의 개수
- Degree(차수) : 해당 노드의 자식노드 개수를 말한다.
트리의 표현
- 중첩된 괄호(Nested Parenthesis) : 같은 레벨의 노드를 괄호로 묶어 표현
- 중첩된 집합(Nested Set) : 트리를 집합관계로 표현
- 들여쓰기(Indentation) : 들여쓰기로 표현된 트리
노드 표현
부모와 자식, 형제노드를 서로 연결짓는 방법
- N-Link(N-링크 표현법) : 노드의 차수가 N개라면 노드가 N개의 링크를 가지고 있어서 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법(단점, 차수가 노드마다 달라지는 트리에서는 적용하기 어렵고 복잡한 트리를 만들게됨)
- Left Child-Right Sibling(왼쪽 자식, 오른쪽 형제 표현법) : N개의 차수를 가진 노드의 표현이 2개의 포인터(링크), 왼쪽-오른쪽 형제만 가진다.
구현
- 노드의 선언
typedef struct _Node {
int data;
struct _Node *left;
struct _Node *right;
}TreeNode;- 노드의 생성
TreeNode* createNode(int data) {
TreeNode newNode = (TreeNode*)malloc(sizeof(TreeNode));
newNode->left = NULL;
newNode->right = NULL;
newNode->data = data;
return newNode;
}- 트리 연결
void addChildNode(TreeNode* parent, TreeNode* child) {
if (parent->left == NULL) {
parent->left = child;
} else {
TreeNode* tmpNode = parent->left;
while(tmpNode->right != null) {
tmpNode = tmpNode->right;
}
tmpNode->right = child;
}
}- 트리 출력
void printTree(TreeNode* node, int depth) {
int i = 0;
for (int i =0; i<depth; i++) {
printf(" ");
}
printf("%d\n", node->data);
if (node->left != NULL) {
printTree(node->left, depth+1);
}
if (node->right != NULL) {
printTree(node->right, depth+1);
}
}
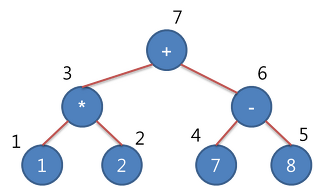
ExpressionTree(수식트리)
- 하나의 연산자가 두 개의 피 연산자를 취한다는 가정아래 두 가지 규칙을 가짐
- 피연산자는 Left Node
- 연산자는 root Node or Branch Node
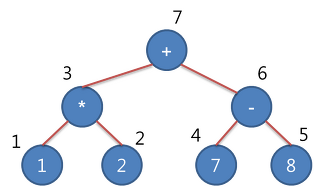
ex) 1 * 2 + (7-8)은 위와 같이 수식트리로 만들 수 있음(후위표기)
알고리즘
- 수식을 뒤에서부터 앞쪽으로 읽어옴
- 수식에서 제일 마지막에 있는 토큰은 루트노드가 된다.
- 후위표기식에서 가장 마지막에 있는 토큰은 항상 연산자이다.
- 수식에서 읽어낸 토큰이 연산자인 경우 가지노드가 되고, 이 토큰 다음에 따라오는 두 개의 토큰은 각각 오른쪽과 왼쪽 자식노드가 된다.
- 다음 토큰에도 연속해서 연산자인 경우 토큰으로부터 만들어지는 하위 트리가 완성된 이후에 읽어낸 토큰이 왼쪽 자식노드가 된다.
- 수식에서 읽어낸 토큰이 숫자이면 Left노드이다.
package algorithm;
import java.math.BigDecimal;
public class ExpTree {
class Node {
private Object data;
private Node left;
private Node right;
public Node() {
data = null;
left = null;
right = null;
}
public Node(Object data) {
this.data = data;
left = null;
right = null;
}
}
public void expressionTree(StringBuilder postFixExp, Node node) {
int len = postFixExp.length();
char token = postFixExp.charAt(len - 1);
postFixExp = postFixExp.deleteCharAt(len - 1);
switch (token) {
case '+':
case '-':
case '*':
case '/':
node = new Node(token);
// Operator
expressionTree(postFixExp, node.right);
expressionTree(postFixExp, node.left);
break;
default:
// Operand
node = new Node(token);
break;
}
}
public double evaluate(Node tree) {
double left = 0;
double right = 0;
double result = 0;
if (tree == null) {
return 0;
}
char data = (char) tree.data;
System.out.println("char data : " + data);
switch (data) {
case '+':
case '-':
case '*':
case '/':
left = evaluate(tree.left);
right = evaluate(tree.right);
if (data == '+') {
result = left + right;
} else if (data == '-') {
result = left - right;
} else if (data == '*') {
result = left * right;
} else if (data == '/') {
result = new BigDecimal(left).divide(new BigDecimal(right)).doubleValue();
}
break;
default:
result = new BigDecimal((char) tree.data).doubleValue();
break;
}
return result;
}
public void postOrderPrint(Node tree) {
if (tree == null) {
return;
}
postOrderPrint(tree.left);
postOrderPrint(tree.right);
System.out.print(tree.data);
}
public void inOrderPrint(Node tree) {
if (tree == null) {
return;
}
System.out.print("(");
inOrderPrint(tree.left);
System.out.print(tree.data);
inOrderPrint(tree.right);
System.out.print(")");
}
}
Binary Tree(이진트리)
- 모든 노드가 최대 2개의 자식노드를 가질 수 있는 트리로 루트 노드를 중심으로 둘로 나뉘는 두 개의 서브 트리도 이진트리어야 하고 하위 트리도 이진트리로 구성되어 있다.
- 최대 노드의 차수는 2이므로 자식 노드가 아예 없거나 하나 또는 둘 뿐이다.
이진트리의 종류
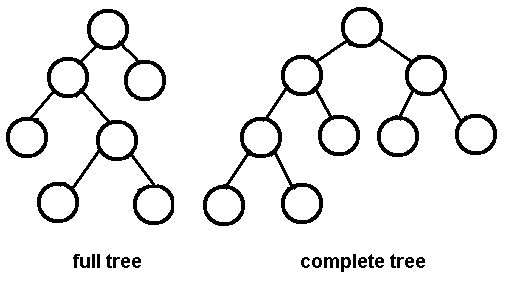
- 포화 이진 트리(Full Binary Tree) : 모든 레벨별로 노드가 꽉 찬 이진 트리를 말한다.
- 완전 이진 트리(Complete Binart Tree) : 포화 이진 트리를 이루기 전 단계의 트리로, 잎 노드들이 왼쪽부터 차곡차곡 채워진 이진 트리이며 모든 노드에 자식 노드가 하나도 없거나 아니면 2개의 자식 노드를 갖는 이진 트리이다.
- 높이 균형 트리(Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1 이상 차이나지 않는 트리
- 완전 높이 균형 트리(Completely Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 트리
이진트리의 순회
- 트리 내 노드들 사이를 돌아다니는 것
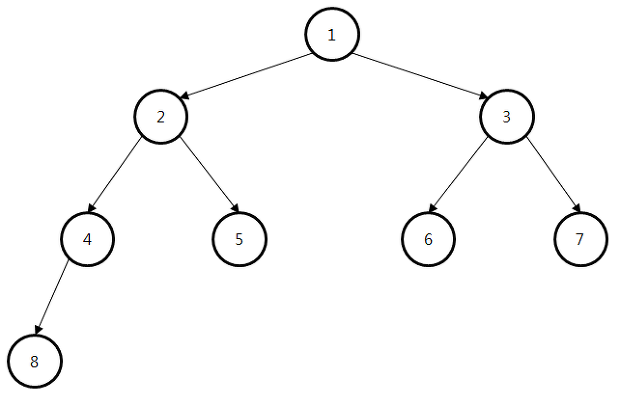
종류
- 전위순회 (Preorder Traversal)
- 방문순서 : root->left->right
- root node 부터 시작하여 아래로 내려오며
- 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위트리를 방문 하는 방식
- 순서 : 1->2->4->8->5->3->6->7
- ( 1( 2(4(8),5), 3( 6, 4) ))
- 중위순회 (Inorder Traversal)
- 방문순서 : left->root->right
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문
- 순서 : 8->4->2->5->1->6->3->7
- 후위순회 (Postorder Traversal)
- 방문순서 : left->right->root
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 하위트리를 거쳐서
- 루트를 방문
- 순서 : 8->4->5->2->6->7->3->1
이진트리 구현
BinaryTre.h
#include <stdio.h>
#include <stdlib.h>
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef char Element;
typedef struct _Node {
struct _Node* left;
struct _Node* right;
Element data;
}TreeNode;
TreeNode* createNode(Element element);
void inOrderTree(TreeNode* node);
void preOrderTree(TreeNode* node);
void postOrderTree(TreeNode* node);
#endif //BINARYTREE_H
BinaryTree.c
//
// Created by Paik Seung Cheol on 2017. 9. 11..
//
#include "BinaryTree.h"
TreeNode* createNode(Element element) {
TreeNode* newNode = (TreeNode*)malloc((sizeof(TreeNode)));
newNode->data = element;
newNode->left = NULL;
newNode->right = NULL;
}
/**
* left->root->right;
* @param node
*/
void inOrderTree(TreeNode* node) {
if (node == NULL)
return;
inOrderTree(node->left);
printf("%c ");
inOrderTree(node->right);
}
/**
* root->left->right;
* @param node
*/
void preOrderTree(TreeNode* node) {
if (node == NULL)
return;
printf("%c ");
preOrderTree(node->left);
preOrderTree(node->right);
}
/**
* left->right->root;
* @param node
*/
void postOrderTree(TreeNode* node) {
if (node == NULL)
return;
postOrderTree(node->left);
inOrderTree(node->right);
printf("%c ");
}
int main() {
TreeNode* rootNode = createNode('A');
TreeNode* BNode = createNode('B');
TreeNode* CNode = createNode('C');
TreeNode* DNode = createNode('D');
TreeNode* ENode = createNode('E');
TreeNode* FNode = createNode('F');
TreeNode* GNode = createNode('G');
rootNode->left = BNode;
rootNode->right = CNode;
BNode->left = DNode;
BNode->right = ENode;
CNode->left = FNode;
CNode->right = GNode;
printf("InOrder : ");
inOrderTree(rootNode);
printf("\\n");
printf("PreOrder : ");
preOrderTree(rootNode);
printf("\\n");
printf("PostOrder : ");
postOrderTree(rootNode);
printf("\\n");
}
Binary Tree(이진트리)
- 모든 노드가 최대 2개의 자식노드를 가질 수 있는 트리로 루트 노드를 중심으로 둘로 나뉘는 두 개의 서브 트리도 이진트리어야 하고 하위 트리도 이진트리로 구성되어 있다.
- 최대 노드의 차수는 2이므로 자식 노드가 아예 없거나 하나 또는 둘 뿐이다.
이진트리의 종류
binaryTree
- 포화 이진 트리(Full Binary Tree) : 모든 레벨별로 노드가 꽉 찬 이진 트리를 말한다.
- 완전 이진 트리(Complete Binart Tree) : 포화 이진 트리를 이루기 전 단계의 트리로, 잎 노드들이 왼쪽부터 차곡차곡 채워진 이진 트리이며 모든 노드에 자식 노드가 하나도 없거나 아니면 2개의 자식 노드를 갖는 이진 트리이다.
- 높이 균형 트리(Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1 이상 차이나지 않는 트리
- 완전 높이 균형 트리(Completely Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 트리
이진트리의 순회
- 트리 내 노드들 사이를 돌아다니는 것
종류
- 전위순회 (Preorder Traversal)
- 방문순서 : root->left->right
- root node 부터 시작하여 아래로 내려오며
- 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위트리를 방문 하는 방식
- 순서 : 1->2->4->8->5->3->6->7
- ( 1( 2(4(8),5), 3( 6, 4) ))
- 중위순회 (Inorder Traversal)
- 방문순서 : left->root->right
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문
- 순서 : 8->4->2->5->1->6->3->7
- 후위순회 (Postorder Traversal)
- 방문순서 : left->right->root
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 하위트리를 거쳐서
- 루트를 방문
- 순서 : 8->4->5->2->6->7->3->1
이진트리 구현
BinaryTre.h
#include <stdio.h>
#include <stdlib.h>
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef char Element;
typedef struct _Node {
struct _Node* left;
struct _Node* right;
Element data;
}TreeNode;
TreeNode* createNode(Element element);
void inOrderTree(TreeNode* node);
void preOrderTree(TreeNode* node);
void postOrderTree(TreeNode* node);
#endif //BINARYTREE_H
BinaryTree.c
//
// Created by Paik Seung Cheol on 2017. 9. 11..
//
#include "BinaryTree.h"
TreeNode* createNode(Element element) {
TreeNode* newNode = (TreeNode*)malloc((sizeof(TreeNode)));
newNode->data = element;
newNode->left = NULL;
newNode->right = NULL;
}
/**
* left->root->right;
* @param node
*/
void inOrderTree(TreeNode* node) {
if (node == NULL)
return;
inOrderTree(node->left);
printf("%c ");
inOrderTree(node->right);
}
/**
* root->left->right;
* @param node
*/
void preOrderTree(TreeNode* node) {
if (node == NULL)
return;
printf("%c ");
preOrderTree(node->left);
preOrderTree(node->right);
}
/**
* left->right->root;
* @param node
*/
void postOrderTree(TreeNode* node) {
if (node == NULL)
return;
postOrderTree(node->left);
inOrderTree(node->right);
printf("%c ");
}
int main() {
TreeNode* rootNode = createNode('A');
TreeNode* BNode = createNode('B');
TreeNode* CNode = createNode('C');
TreeNode* DNode = createNode('D');
TreeNode* ENode = createNode('E');
TreeNode* FNode = createNode('F');
TreeNode* GNode = createNode('G');
rootNode->left = BNode;
rootNode->right = CNode;
BNode->left = DNode;
BNode->right = ENode;
CNode->left = FNode;
CNode->right = GNode;
printf("InOrder : ");
inOrderTree(rootNode);
printf("\\n");
printf("PreOrder : ");
preOrderTree(rootNode);
printf("\\n");
printf("PostOrder : ");
postOrderTree(rootNode);
printf("\\n");
}
반응형
'Algorithms > structure' 카테고리의 다른 글
| 7. Priority Queue(우선순위 큐) (0) | 2023.04.18 |
|---|---|
| 6. Hash(해시) (0) | 2023.04.18 |
| 4. Queue(큐) (0) | 2023.04.17 |
| 3. Stack(스택) (0) | 2023.04.17 |
| 2. Linked List(연결리스트) (0) | 2023.04.17 |
반응형
Tree(트리)
- 나무와 유사하게 비선형(데이터가 계층적 구조로 이루어짐) 구조로 이루어져 있는 자료구조
- 트리는 다른 자료구조보다 자료를 저장하거나 검색하는 방법이 간단하고 메모리를 효율적으로 사용할 수 있다.
구성
- 트리는 크게 Root(뿌리), Branch(가지),leaf(잎) 세 가지 요소로 이루어짐
- Root : 트리 구조에서 최상위에 존재하는 노드이다.
- Branch : Root Node or Sub Tree 와 leaf 사이에 있는 노드를 말한다(자식).
- Leaf(Terminal Node) : Branch Node의 맨 끝에 달려있는 노드로, 밑으로 또 다른 노드가 연결되어 있지 않은 노드를 말한다(Terminal(단말)노드).
- Node : 트리의 구성요소에 해당하는 요소를 말한다.
- Edge : 노드와 노드를 연결하는 연결선이다.
- Sub-Tree : 큰 트리(전체)에 속하는 작은 트리
- Level(Depth) : 루트노드에서 해당 노드까지 경로의 길이로 트리에서 각 층별로 숫자를 매김
- Height : 트리의 최고 레벨 (3)
- Length : 출발 노드에서 목적 노드까지 거쳐야하는 노드의 개수
- Degree(차수) : 해당 노드의 자식노드 개수를 말한다.
트리의 표현
- 중첩된 괄호(Nested Parenthesis) : 같은 레벨의 노드를 괄호로 묶어 표현
- 중첩된 집합(Nested Set) : 트리를 집합관계로 표현
- 들여쓰기(Indentation) : 들여쓰기로 표현된 트리
노드 표현
부모와 자식, 형제노드를 서로 연결짓는 방법
- N-Link(N-링크 표현법) : 노드의 차수가 N개라면 노드가 N개의 링크를 가지고 있어서 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법(단점, 차수가 노드마다 달라지는 트리에서는 적용하기 어렵고 복잡한 트리를 만들게됨)
- Left Child-Right Sibling(왼쪽 자식, 오른쪽 형제 표현법) : N개의 차수를 가진 노드의 표현이 2개의 포인터(링크), 왼쪽-오른쪽 형제만 가진다.
구현
- 노드의 선언
typedef struct _Node {
int data;
struct _Node *left;
struct _Node *right;
}TreeNode;- 노드의 생성
TreeNode* createNode(int data) {
TreeNode newNode = (TreeNode*)malloc(sizeof(TreeNode));
newNode->left = NULL;
newNode->right = NULL;
newNode->data = data;
return newNode;
}- 트리 연결
void addChildNode(TreeNode* parent, TreeNode* child) {
if (parent->left == NULL) {
parent->left = child;
} else {
TreeNode* tmpNode = parent->left;
while(tmpNode->right != null) {
tmpNode = tmpNode->right;
}
tmpNode->right = child;
}
}- 트리 출력
void printTree(TreeNode* node, int depth) {
int i = 0;
for (int i =0; i<depth; i++) {
printf(" ");
}
printf("%d\n", node->data);
if (node->left != NULL) {
printTree(node->left, depth+1);
}
if (node->right != NULL) {
printTree(node->right, depth+1);
}
}
ExpressionTree(수식트리)
- 하나의 연산자가 두 개의 피 연산자를 취한다는 가정아래 두 가지 규칙을 가짐
- 피연산자는 Left Node
- 연산자는 root Node or Branch Node

ex) 1 * 2 + (7-8)은 위와 같이 수식트리로 만들 수 있음(후위표기)
알고리즘
- 수식을 뒤에서부터 앞쪽으로 읽어옴
- 수식에서 제일 마지막에 있는 토큰은 루트노드가 된다.
- 후위표기식에서 가장 마지막에 있는 토큰은 항상 연산자이다.
- 수식에서 읽어낸 토큰이 연산자인 경우 가지노드가 되고, 이 토큰 다음에 따라오는 두 개의 토큰은 각각 오른쪽과 왼쪽 자식노드가 된다.
- 다음 토큰에도 연속해서 연산자인 경우 토큰으로부터 만들어지는 하위 트리가 완성된 이후에 읽어낸 토큰이 왼쪽 자식노드가 된다.
- 수식에서 읽어낸 토큰이 숫자이면 Left노드이다.
package algorithm;
import java.math.BigDecimal;
public class ExpTree {
class Node {
private Object data;
private Node left;
private Node right;
public Node() {
data = null;
left = null;
right = null;
}
public Node(Object data) {
this.data = data;
left = null;
right = null;
}
}
public void expressionTree(StringBuilder postFixExp, Node node) {
int len = postFixExp.length();
char token = postFixExp.charAt(len - 1);
postFixExp = postFixExp.deleteCharAt(len - 1);
switch (token) {
case '+':
case '-':
case '*':
case '/':
node = new Node(token);
// Operator
expressionTree(postFixExp, node.right);
expressionTree(postFixExp, node.left);
break;
default:
// Operand
node = new Node(token);
break;
}
}
public double evaluate(Node tree) {
double left = 0;
double right = 0;
double result = 0;
if (tree == null) {
return 0;
}
char data = (char) tree.data;
System.out.println("char data : " + data);
switch (data) {
case '+':
case '-':
case '*':
case '/':
left = evaluate(tree.left);
right = evaluate(tree.right);
if (data == '+') {
result = left + right;
} else if (data == '-') {
result = left - right;
} else if (data == '*') {
result = left * right;
} else if (data == '/') {
result = new BigDecimal(left).divide(new BigDecimal(right)).doubleValue();
}
break;
default:
result = new BigDecimal((char) tree.data).doubleValue();
break;
}
return result;
}
public void postOrderPrint(Node tree) {
if (tree == null) {
return;
}
postOrderPrint(tree.left);
postOrderPrint(tree.right);
System.out.print(tree.data);
}
public void inOrderPrint(Node tree) {
if (tree == null) {
return;
}
System.out.print("(");
inOrderPrint(tree.left);
System.out.print(tree.data);
inOrderPrint(tree.right);
System.out.print(")");
}
}
Binary Tree(이진트리)
- 모든 노드가 최대 2개의 자식노드를 가질 수 있는 트리로 루트 노드를 중심으로 둘로 나뉘는 두 개의 서브 트리도 이진트리어야 하고 하위 트리도 이진트리로 구성되어 있다.
- 최대 노드의 차수는 2이므로 자식 노드가 아예 없거나 하나 또는 둘 뿐이다.
이진트리의 종류

- 포화 이진 트리(Full Binary Tree) : 모든 레벨별로 노드가 꽉 찬 이진 트리를 말한다.
- 완전 이진 트리(Complete Binart Tree) : 포화 이진 트리를 이루기 전 단계의 트리로, 잎 노드들이 왼쪽부터 차곡차곡 채워진 이진 트리이며 모든 노드에 자식 노드가 하나도 없거나 아니면 2개의 자식 노드를 갖는 이진 트리이다.
- 높이 균형 트리(Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1 이상 차이나지 않는 트리
- 완전 높이 균형 트리(Completely Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 트리
이진트리의 순회
- 트리 내 노드들 사이를 돌아다니는 것

종류
- 전위순회 (Preorder Traversal)
- 방문순서 : root->left->right
- root node 부터 시작하여 아래로 내려오며
- 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위트리를 방문 하는 방식
- 순서 : 1->2->4->8->5->3->6->7
- ( 1( 2(4(8),5), 3( 6, 4) ))
- 중위순회 (Inorder Traversal)
- 방문순서 : left->root->right
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문
- 순서 : 8->4->2->5->1->6->3->7
- 후위순회 (Postorder Traversal)
- 방문순서 : left->right->root
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 하위트리를 거쳐서
- 루트를 방문
- 순서 : 8->4->5->2->6->7->3->1
이진트리 구현
BinaryTre.h
#include <stdio.h>
#include <stdlib.h>
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef char Element;
typedef struct _Node {
struct _Node* left;
struct _Node* right;
Element data;
}TreeNode;
TreeNode* createNode(Element element);
void inOrderTree(TreeNode* node);
void preOrderTree(TreeNode* node);
void postOrderTree(TreeNode* node);
#endif //BINARYTREE_H
BinaryTree.c
//
// Created by Paik Seung Cheol on 2017. 9. 11..
//
#include "BinaryTree.h"
TreeNode* createNode(Element element) {
TreeNode* newNode = (TreeNode*)malloc((sizeof(TreeNode)));
newNode->data = element;
newNode->left = NULL;
newNode->right = NULL;
}
/**
* left->root->right;
* @param node
*/
void inOrderTree(TreeNode* node) {
if (node == NULL)
return;
inOrderTree(node->left);
printf("%c ");
inOrderTree(node->right);
}
/**
* root->left->right;
* @param node
*/
void preOrderTree(TreeNode* node) {
if (node == NULL)
return;
printf("%c ");
preOrderTree(node->left);
preOrderTree(node->right);
}
/**
* left->right->root;
* @param node
*/
void postOrderTree(TreeNode* node) {
if (node == NULL)
return;
postOrderTree(node->left);
inOrderTree(node->right);
printf("%c ");
}
int main() {
TreeNode* rootNode = createNode('A');
TreeNode* BNode = createNode('B');
TreeNode* CNode = createNode('C');
TreeNode* DNode = createNode('D');
TreeNode* ENode = createNode('E');
TreeNode* FNode = createNode('F');
TreeNode* GNode = createNode('G');
rootNode->left = BNode;
rootNode->right = CNode;
BNode->left = DNode;
BNode->right = ENode;
CNode->left = FNode;
CNode->right = GNode;
printf("InOrder : ");
inOrderTree(rootNode);
printf("\\n");
printf("PreOrder : ");
preOrderTree(rootNode);
printf("\\n");
printf("PostOrder : ");
postOrderTree(rootNode);
printf("\\n");
}
Binary Tree(이진트리)
- 모든 노드가 최대 2개의 자식노드를 가질 수 있는 트리로 루트 노드를 중심으로 둘로 나뉘는 두 개의 서브 트리도 이진트리어야 하고 하위 트리도 이진트리로 구성되어 있다.
- 최대 노드의 차수는 2이므로 자식 노드가 아예 없거나 하나 또는 둘 뿐이다.
이진트리의 종류
binaryTree
- 포화 이진 트리(Full Binary Tree) : 모든 레벨별로 노드가 꽉 찬 이진 트리를 말한다.
- 완전 이진 트리(Complete Binart Tree) : 포화 이진 트리를 이루기 전 단계의 트리로, 잎 노드들이 왼쪽부터 차곡차곡 채워진 이진 트리이며 모든 노드에 자식 노드가 하나도 없거나 아니면 2개의 자식 노드를 갖는 이진 트리이다.
- 높이 균형 트리(Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 1 이상 차이나지 않는 트리
- 완전 높이 균형 트리(Completely Height Balanced Tree) : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 트리
이진트리의 순회
- 트리 내 노드들 사이를 돌아다니는 것
종류
- 전위순회 (Preorder Traversal)
- 방문순서 : root->left->right
- root node 부터 시작하여 아래로 내려오며
- 왼쪽 하위 트리의 방문이 끝나면
- 오른쪽 하위트리를 방문 하는 방식
- 순서 : 1->2->4->8->5->3->6->7
- ( 1( 2(4(8),5), 3( 6, 4) ))
- 중위순회 (Inorder Traversal)
- 방문순서 : left->root->right
- 왼쪽 하위 트리부터 시작해서
- 루트를 거쳐
- 오른쪽 하위 트리를 방문
- 순서 : 8->4->2->5->1->6->3->7
- 후위순회 (Postorder Traversal)
- 방문순서 : left->right->root
- 왼쪽 하위 트리부터 시작해서
- 오른쪽 하위트리를 거쳐서
- 루트를 방문
- 순서 : 8->4->5->2->6->7->3->1
이진트리 구현
BinaryTre.h
#include <stdio.h>
#include <stdlib.h>
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef char Element;
typedef struct _Node {
struct _Node* left;
struct _Node* right;
Element data;
}TreeNode;
TreeNode* createNode(Element element);
void inOrderTree(TreeNode* node);
void preOrderTree(TreeNode* node);
void postOrderTree(TreeNode* node);
#endif //BINARYTREE_H
BinaryTree.c
//
// Created by Paik Seung Cheol on 2017. 9. 11..
//
#include "BinaryTree.h"
TreeNode* createNode(Element element) {
TreeNode* newNode = (TreeNode*)malloc((sizeof(TreeNode)));
newNode->data = element;
newNode->left = NULL;
newNode->right = NULL;
}
/**
* left->root->right;
* @param node
*/
void inOrderTree(TreeNode* node) {
if (node == NULL)
return;
inOrderTree(node->left);
printf("%c ");
inOrderTree(node->right);
}
/**
* root->left->right;
* @param node
*/
void preOrderTree(TreeNode* node) {
if (node == NULL)
return;
printf("%c ");
preOrderTree(node->left);
preOrderTree(node->right);
}
/**
* left->right->root;
* @param node
*/
void postOrderTree(TreeNode* node) {
if (node == NULL)
return;
postOrderTree(node->left);
inOrderTree(node->right);
printf("%c ");
}
int main() {
TreeNode* rootNode = createNode('A');
TreeNode* BNode = createNode('B');
TreeNode* CNode = createNode('C');
TreeNode* DNode = createNode('D');
TreeNode* ENode = createNode('E');
TreeNode* FNode = createNode('F');
TreeNode* GNode = createNode('G');
rootNode->left = BNode;
rootNode->right = CNode;
BNode->left = DNode;
BNode->right = ENode;
CNode->left = FNode;
CNode->right = GNode;
printf("InOrder : ");
inOrderTree(rootNode);
printf("\\n");
printf("PreOrder : ");
preOrderTree(rootNode);
printf("\\n");
printf("PostOrder : ");
postOrderTree(rootNode);
printf("\\n");
}
반응형
'Algorithms > structure' 카테고리의 다른 글
| 7. Priority Queue(우선순위 큐) (0) | 2023.04.18 |
|---|---|
| 6. Hash(해시) (0) | 2023.04.18 |
| 4. Queue(큐) (0) | 2023.04.17 |
| 3. Stack(스택) (0) | 2023.04.17 |
| 2. Linked List(연결리스트) (0) | 2023.04.17 |