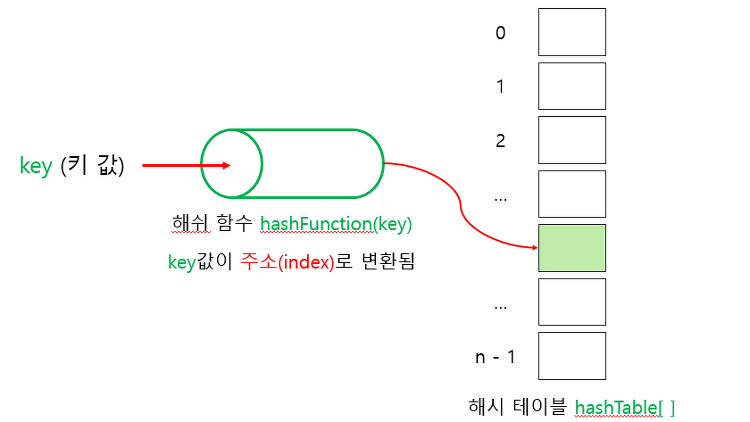
Hash(해시)
정의
- 인덱스를 사용하는 알고리즘으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수이다
- 데이터를 입력받고 완전히 다른 모습의 데이터로 바꾸어 놓는 작업
- 잘게 부수고 다시 뭉치는 것
- 대용량의 데이터를 검색할 때 주로 사용
- 효율적인 탐색 알고리즘을 위한 자료구조로써 Key를 Value에 대응시킨다.
사전구조 개념
- 사전구조는 map이나 table로 불리고 key와 value 두 가지 종류의 필드를 가진다.
- 데이터에 접근하고 삭제할 때 탐색할 key값만 알 수 있으면 된다.
해시의 사용용도
- 해시테이블(Hash Table) : 데이터의 해시 값을 테이블 내의 주소로 이용하는 궁극의 탐색 알고리즘이다.
- 암호화 : 해시는 입력받은 데이터를 완전히 새로운 모습의 데이터로 만든다.(ex- SHA:Secure Hash Algorithm)
- 데이터 축약 : 길이가 서로 다른 입력 데이터에 대해 일정한 길이의 출력을 만들 수 있다. 이 특성을 이용하여 데이터를 ’해시’하면 짧은 길이로 축약할 수 있다.
해시 알고리즘의 용어
- Bucket(버킷) : 해시주소 하나에 1개 이상의 데이터가 저장되는 전체 메모리공간
- Slot(슬롯) : 버킷에서 하나의 데이터가 저장되는 메모리 공간
- Collision(충돌) : 서로 다른 데이터인데 같은 해시주소를 갖게되면 충돌이 발생된다.
- Overflow(오버플로) : 충돌을 예방하기위해 해시주소 1개에 여러 개의 슬롯을 만든다. 그러나 충돌이 계속 발생해서 더 이상 데이터를 저장할 슬롯이 없어지는 상황이 발생하면 오버플로가 발생
- Cluster(클러스터) : 해시 테이블 내의 일부 지역들의 주소를 집중적으로 반환하는 결과로 한 곳에 모이는 문제
해시 테이블 (Hash Table)
- 키 값의 연산에 의해 직접 접근이 가능한 구조로써, 데이터를 담을 테이블을 미리 확보한 후 입력 받은 데이터를 해시(데이터를 잘게 부수고 다시 뭉쳐)하여 테이블 내의 주소를 계산하고 이 주소를 데이터에 담는 것이다.
- 해시테이블은 데이터가 입력되지 않은 공간이 많아야 제 성능을 유지할 수 있다.
해시 함수(Hash function)
- Devision Method(나눗셈법) : 입력 값을 테이블의 크기로 나누고 나머지를 테이블 주소로 사용
- 주소 = 입력 값 % 테이블 크기
- 입력 값이 테이블 크기의 배수 또는 약수인 경우 0을 반환
- 그렇지 않는 경우 n-1을 반환
- 서로 다른 입력 값에 대해 동일한 해시 값, 즉 해시 테이블 내의 동일한 주소를 반환할 가능성이 높음(이것을 충돌(Collision)이라고 함)
- Digits Folding(자릿수 접기) : Collision or Cluster를 줄일 수 있는 알고리즘으로 일정크기 이하의 수로 만드는 방법이다.
- 10진수의 경우 0~9까지 값을 값을 가지므로 한 자리수 접기는 최대 63개 두 자리수 접기는 306까지의 해시 값을 얻을 수 있다.
- Digits Folding은 문자열을 키로 사용하는 해시 테이블에 잘 어울림.
int Digit_Folding_Hash(char* key, int length, int tableSize) {
int i = 0;
int hashValue = 0;
for (i = 0; i<length; i++) {
hashValue += key[i];
}
return hashValue % tableSize;- 문자열 키를 Digits Folding 알고리즘을 통해 키를 만들어내는 코드
- 문자열의 최대길이가 10자리면 해시함수는 10 * 127 1270이므로 1271 사이의 주소는 활용되지 않는다. ASCII로 10자리를 만들었을 때 조합할 수 있는 경우의 수가 127^10 가지나 됨
- 테이블 크기를 2진수로 표현하고 해시 값을 3비트씩 밀어올린 후 ASCII코드 번호를 더하면 해시테이블의 폐가 문제를 해결할 수 있다.
int Digit_Folding_Hash(char* key, int length, int tableSize) {
int i = 0;
int hashValue = 0;
for (i = 0; i<length; i++) {
hashValue = (hashValue << 3) + key[i];
}
return hashValue % tableSize;
}
ex) 7자리의 숫자 819335각 한 자릿수를 더한다
8+1+9+3+3+5 = 31
새로운 값 31이 나온다.
819335는 31로 일정 크기 이하의 수가 나왔다.두 자리씩 더할 경우
81 + 93 + 35 = 148
새로운 값 148이 나옴.
- 해시 함수의 한계
- 해시 함수가 서로 다른 입력 값에 대해 동일한 해시 테이블 주소를 반환하는 것을 ‘Collision’ 이라고 한다.
해싱 (Hashing)
- 해시 테이블을 이용한 탐색 이라고하며, 키 값에 직접 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 접근하는 자료구조. 해시 테이블(Hash Table) 은 키 값의 연산에 의한 직접 접근이 가능한 구조로 해시 테이블(Hash Table)을 이용한 탐색을 해싱(Hashin) 이라고 한다.
- 어떤항목의 탐색 키만을 가지고 바로 항목이 저장되어 있는 배열의 인덱스를 결정하는 기법.
해싱의 구조
해싱은 자료를 저장하는데 배열을 사용한다. 원하는 항목이 저장된 위치를 알고 있다면 빠르게 삽입하거나 꺼낼 수 있다.
- 해시함수(Hash Function) : 탐색 키를 입력받아 해시 주소(Hash Address) 를 생성하고 해시 주소가 배열로 구현된 해시 테이블(Hash Table) 의 인덱스가 된다.
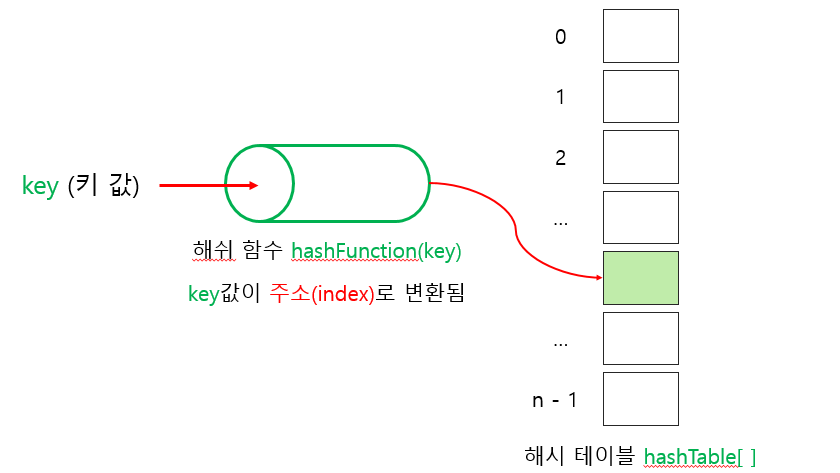
- 해시 테이블 K를 받아서 해시 함수 h()로 연산한 결과인 해시 주소 h(k)를 인덱스로 사용하여 해시 테이블에 있는 항목에 접근한다.
- 해시테이블 ht는 M개의 버켓(bucket) 으로 이루어지는 테이블로써 ht[0], ht[1]… ht[M-1]의 원소를 가진다.
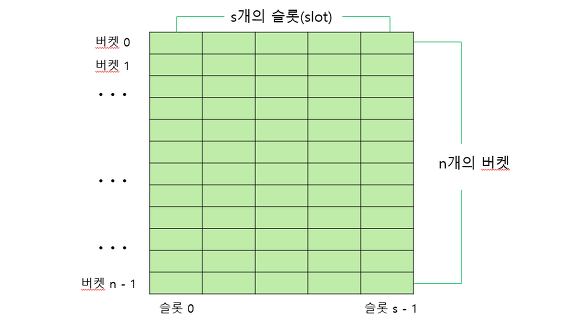
- 버켓은 s개의 슬롯(slot) 을 가질 수 있으며, 하나의 슬롯에는 하나의 항목이 저장된다. 하나의 버켓에 여러 개의 슬롯을 두는 이유는 서로 다른 두 개의 키가 해시 함수에 의해 동일한 주소로 변환될 수 있으므로 여러 개의 항목을 동일한 버켓에 저장하기 위해서이지만, 대부분의 경우 하나의 버켓에 하나의 슬롯을 가진다.
- 해시테이블에 존재하는 버켓의 수가 M이므로 해시 함수 h()는 모든 k에 대해 0 ≤ h(k) ≤ M − 1 의 범위 값을 제공해야한다. 대부분의 경우 해시 테이블의 버켓 수는 키가 가질 수 있는 모든 경우의 수보다 매우 작으므로 여러 개의 서로 다른 탐색 키가 해시 함수에 의해 같은 해시 구조로 사상(Mapping)되는 경우가 자주 발생한다.
- 서로다른 두 개의 탐색 키 K1와 K2에 대하여 h(k1) = h(k2)인 경우를 충돌(Collision) 이라고 한며, 이러한 키 k1, k2를 동의어(synonym) 라 한다.
- 만약 충돌이 발생하면 같은 버켓에 있는 다른 슬롯에 항목을 저장하게 된다.
- 충돌이 자주 일어나면 버켓 내부에서 순차탐색 시간이 길어져 탐색 성능이 저하될 수 있으므로 해시 함수를 수정하거나 해시 테이블의 크기를 적절하게 조절해야한다.
- 충돌이 버켓에 할당된 슬롯 수보다 많이 발생하게 되면 버켓에 더 이상 항목을 저장할 수 없게 되는 오버플로(overflow)가 발생한다. 만약 버켓당 슬롯의 수가 하나(s==1)이면 충돌이 곧 오버플로를 의미한다.
- 오버플로가 발생하면 더 이상 항목을 저장할 수 없으므로 오버플로를 해결하기 위한 방법이 반드시 필요.
해시 알고리즘에서 발생되는 문제들
- 테이블 해시주소의 중복
- 버킷 용량
- 오버플로 해결
- 개방주소법(Open Address) : 해시 함수에 의해 얻어진 주소가 아니더라도 다른 주소를 사용할 수 있도록 허용하는 충돌해결 알고리즘
- 선형조사방법(Linear Proving Method) : 현재 만들어진 해시 주소로 데이터를 넣으려는데 이미 꽉 채워져 있으면 바로 옆자리를 확인하고 옆자리도 채워져 있다면 다시 옆자리로 이동하며 작업을 반복하는 알고리즘
- 구현방법간단, 성능도 soso
- 같은 해시주소를 사용해서 충돌이 발생할 때마다 원래의 해시주소 근처의 주소에 데이터가 집중되는 현상 발생
- 클러스터링(솔림현상)이 발생
- 제곱탐사(Quadratic Probing) : 선형 탐사는 다음 주소를 찾기 위해 고정폭만큼 이동하지만 제곱탐사는 이동폭이 제곱수로 늘어는 것.
- 선형조사방법(Linear Proving Method) : 현재 만들어진 해시 주소로 데이터를 넣으려는데 이미 꽉 채워져 있으면 바로 옆자리를 확인하고 옆자리도 채워져 있다면 다시 옆자리로 이동하며 작업을 반복하는 알고리즘
- 이중해싱(Double Hashing) : 첫 번째 해시함수에서 충돌이 발생할 경우 이동폭을 더하여 다른 해시 함수를 이용하는 것 (테이블의 끝을 만나면 처음부터 다시 탐색)
- 폐쇄주소법(Closed Address) :
- 분리연결법(eperate Chaining) : 연결리스트(Linked List) : 연결리스트를 사용하여 오버플로가 발생하더라도 다른 해시 주소로 이동하지 않고 해당 주소안에 새로운 노드를 생성하여 연결한다. 해시주소는 바뀌지 않는 장점이 있지만 클러스터링이 발생하면 연결리스트 내부에서 검색 작업이 발생한다.
- 리해싱(Rehashing) : 해시 테이블의 크기를 늘리고, 늘어난 해시 테이블의 크기에 맞추어 테이블 내의 모든 데이터를 다시 해싱하는 것
- 개방주소법(Open Address) : 해시 함수에 의해 얻어진 주소가 아니더라도 다른 주소를 사용할 수 있도록 허용하는 충돌해결 알고리즘
해시 알고리즘의 효율성은 해시 함수가 얼마나 복잡한지에 따라 달라진다.
또한 해시 함수 역시 해시 주소를 어떻게 결정할 것인지 또는 Key의 패턴이 어떤지에 따라 달라진다.
충돌 해결하기
- 개방 해싱(Open Hashing) : 해시 테이블의 바깥에 새로운 공간을 할당하여 문제를 수습
- 폐쇄 해싱(Closed Hashing) : 처음에 주어진 해시 테이블 공간에서 문제를 해결
- 체이닝(Chaining) : 해시 함수가 서로 다른 키에 대해 같은 주소값을 반환해서 충돌이 발생하면 각 데이터를 해당 주소에 있는 연결 리스트에 삽입하여 문제를 해결하는 기법
- 체이닝 가반의 해시 테이블은 데이터 대신 연결리스트에 대한 포인터를 관리
- 삽입연산은 충돌이 앞으로 발생할 것을 고려하여 설계
- 삭제, 탐색 연산은 이미 충돌이 발생했을 것을 고려하여 설계
- 체이닝은 오픈 해싱 기법인 동시에 폐쇄 주소법 알고리즘이기도 한다.
체이닝의 탐색순서
- 찾고자하는 목표값을 해싱하여 연결 리스트가 저장되어 있는 주소를 찾음
- 이 주소를 이용하여 해시 테이블에 저장되어 있는 연결리스트에 대한 포인터를 생성
- 연결 리스트 앞에서부터 뒤까지 차례로 이동하며 목표 값이 저장되어 있는지 비교
- 목표값과 연결 리스트 내의 노드 값이 일치하면 해당 노드주소 반환
체이닝의 문제점 및 해결 방법
문제점
- 체이닝은 원하는 데이터를 찾기 위해서 순차탐색을 해야하는 연결리스트의 단점을 가지고 있다.
해결방법
- 레드 블랙 트리 또는 이진탐색 트리를 이용하면 문제를 해결 할 수 있다.
Key-Address 검색 알고리즘
- 인덱스만으로 원하는 데이터를 검색하는 알고리즘이다.
- 비유 : 아파트 우편함 동 호수에 내용물이 담겨있는 것처 해당 key에 데이터가 담겨있는 것을 말함
- O(1) 의 성능을 낸다.
void keyAddress() {
int i = 0;
for (i = 0; i<5; i++) {
student->name ='A'+i;
student->number = 1000+i;
printf("%학번 : %d 이름 : %c\n", student->number, student->name);
}
}위 코드처럼 배열의 인덱스만 알면 비교나 검색할 필요가 없이 해당 데이터에 학번 이름을 출력할 수 있다. 그러나 메모리의 효율성은 떨어진다. 전체 데이터의 크기는 10 바이트라면 저장된 데이터 크미는 5바이트 밖에 사용하지 않았기 때문이다.
Key-Mapping 검색 알고리즘
- Key-Address의 단점을 해결해주는 알고리즘으로 찾고자 하는 데이터를 나눈 나머지 값을 구하는 기능
- 문제점 : 데이터가 중복될 수 있다.
void MakeKeyMapping() {
int i=0, num, idx;
srand((unsigned)time(NULL));
while(i < 50) {
num = rand() % 100;
Buf[num] = num % 50;
idx = num % 50;
Hit[idx].key = idx;
Hit[idx].counter++;
i++;
}
}추상자료형
- 새로운 항목을 사입(add)
- 탐색 키에 관련된 항목을 삭제(delete)
- 탐색 키에 관련된 값을 탐색(search)
- 객체 : 일련의 (key, value) 쌍의 집합
- 연산
- add(key, value) : (key, value)를 사전에 추가
- delete(key) : key에 해당되는 (key, value)를 찾아서 삭제하고 관련된 value는 반환한다. 탐색에 실패하면 null을 반환
- search(key) : key에 해당되는 value를 찾아서 반환. 만약 탐색이 실패하면 null을 반환
ex)
Hash.h
#ifndef HASH_H
#define HASH_H
#include <Stdio.h>
#include <stdlib.h>
#include <memory.h>
#include <string.h>
typedef char* KeyType;
typedef char* ValueType;
typedef struct _tagNode {
KeyType key;
ValueType value;
struct _tagNode *next;
}Node;
typedef Node* List;
typedef struct _HashTable {
int tableSize;
List* table;
}_HashTable;
typedef struct tagHashTable {
int tableSize;
Node* table;
}HashTable;
HashTable* SHT_createHashTable(int tableSize);
void SHT_Put(HashTable* HT, KeyType key, ValueType value);
ValueType SHT_Get(HashTable* HT, KeyType key);
void SHT_DestoryHashTable(HashTable* HT);
int SHT_Hash(int input, int tblSize);
int Digit_Folding_Hash(char* key, int length, int tableSize);
HashTable* CHT_CreateHashTable(int tableSize);
void CHT_DestoryHashTable(_HashTable* HT);
Node* CHT_CreateNode(KeyType key, ValueType value);
void CHT_DestoryList(List List);
void CHT_DestoryNode(Node* node);
void CHT_Set(_HashTable* HT, KeyType key, ValueType value);
int CHT_Hash(KeyType key ,int length, int tableSize);
ValueType CHT_Get(_HashTable* HT, KeyType key);
#endif //HASH_H나눗셈법을 이용한 hashtable
SimpleHashTable.c
#include "Hash.h"
HashTable* SHT_createHashTable(int tableSize) {
HashTable* HT = (HashTable*)malloc(sizeof(HashTable));
HT->table = (Node*)malloc(sizeof(Node)* tableSize);
HT->tableSize = tableSize;
return HT;
}
void SHT_Put(HashTable* HT, KeyType key, ValueType value) {
int adr = SHT_Hash(key, HT->tableSize);
HT->table[adr].key = key;
HT->table[adr].value = value;
}
ValueType SHT_Get(HashTable* HT, KeyType key) {
int adr = SHT_Hash(key, HT->tableSize);
return HT->table[adr].value;
}
void SHT_DestoryHashTable(HashTable* HT) {
free(HT->table);
free(HT);
}
int SHT_Hash(int input, int tblSize) {
return input % tblSize;
}체이닝을 이용한 해시
#include "Hash.h"
int CHT_Hash(KeyType key ,int length, int tableSize) {
int hashKey = 0;
int i = 0 ;
for (i = 0; i<length; i++) {
hashKey = (hashKey << 3) + key[i];
}
return hashKey % tableSize;
}
void CHT_Set(_HashTable* HT, KeyType key, ValueType value) {
int idx = CHT_Hash(key, strlen(key), HT->tableSize);
Node* newNode = CHT_CreateNode(key,value);
if (HT->table[idx] == NULL) {
HT->table[idx] = newNode;
printf("put : key(%s), idx(%d)\n", key,idx);
} else {
List list = HT->table[idx];
newNode->next = list;
HT->table[idx] = newNode;
printf("Collision occured : key(%s), idx(%d)\n", key,idx);
}
}
ValueType CHT_Get(_HashTable* HT, KeyType key) {
int idx = CHT_Hash(key, strlen(key), HT->tableSize);
List list = HT->table[idx];
List Target = NULL;
if (list == NULL) {
return NULL;
}
while(1) {
if (strcmp(list->key, key) == 0) {
Target = list;
break;
}
if (list->next == NULL) {
break;
}
else {
list = list->next;
}
}
return Target->value;
}
HashTable* CHT_CreateHashTable(int tableSize) {
_HashTable* hashTable = (_HashTable*)malloc((sizeof(_HashTable)));
hashTable->table = (List*)malloc((sizeof(List) * tableSize));
memset(hashTable->table,0, sizeof(List) *tableSize);
hashTable->tableSize = tableSize;
return hashTable;
}
Node* CHT_CreateNode(KeyType key, ValueType value) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->value = value;
newNode->key = key;
newNode->next = NULL;
return newNode;
}
void CHT_DestoryHashTable(_HashTable* HT) {
int i =0;
for (i=0;i<HT->tableSize; i++) {
List L = HT->table[i];
CHT_DestoryList(L);
}
free(HT->table);
free(HT);
}
void CHT_DestoryNode(Node* node) {
free(node->key);
free(node->value);
free(node);
}
void CHT_DestoryList(List list) {
if (list == NULL) {
return;
}
if (list->next != NULL) {
CHT_DestoryList(list->next);
}
CHT_DestoryNode(list);
}선형탐색법 사용, 이중 해싱, 리해싱.
public class HashTable implements Hash {
private TagHashTable hash;
public HashTable() {
this.hash = new TagHashTable();
}
public HashTable(int capacity) {
this.hash = new TagHashTable(capacity);
}
private class TagHashTable {
Node[] table = null;
private int capacity = 0;
private int hashTableCount = 0;
private static final int DEFAULT_CAPACITY = 100;
public TagHashTable(int capacity) {
this.capacity = capacity;
this.hashTableCount = 0;
this.table = new Node[this.capacity];
}
public TagHashTable() {
this.capacity = DEFAULT_CAPACITY;
this.hashTableCount = 0;
this.table = new Node[this.capacity];
}
}
private class Node {
private int key;
private Object value;
private boolean usaged;
public Node() {
this.key = 0;
this.value = null;
this.usaged = false;
}
public Node(int key, Object value) {
this.key = key;
this.value = value;
this.usaged = false;
}
}
/**
* 1. 해시테이블 크기 계산
* 2. 해시테이블 크기가 50%가 넘으면 리해싱
* 3. 중복키 확인
* 4. 해시 적용
*/
@Override
public void put(String key, Object value) {
if (isHashSizeOver()) {
rehashing();
}
int key1 = hash(key, key.length(), hash.capacity);
int key2 = hash2(key, key.length(), hash.capacity);
while (hash.table[key1] != null && hash.table[key1].usaged != false && hash.table[key1].key != key1) {
key1 = (key1 + key2) % hash.capacity;
}
Node newNode = new Node();
newNode.key = key1;
newNode.value = value;
newNode.usaged = true;
hash.table[key1] = newNode;
hash.hashTableCount++;
}
@Override
public Object get(String key) {
int key1 = hash(key, key.length(), hash.capacity);
int key2 = hash(key, key.length(), hash.capacity);
while(hash.table[key1] != null && hash.table[key1].usaged != false && hash.table[key1].key != key1) {
key1 = (key1 + key2) % hash.capacity;
}
return hash.table[key1].value;
}
@Override
public void remove(String key) {
}
private int hash(String key, int length, int capacity) {
int hashKey = 0;
for (int i =0; i<length; i++) {
hashKey = (hashKey << 3) + key.charAt(i);
}
return hashKey % capacity;
}
private int hash2(String key, int length, int capacity) {
int hashKey = 0;
for (int i =0; i<length; i++) {
hashKey = (hashKey << 3) + key.charAt(i);
}
return (hashKey % (capacity -3) ) + 1;
}
private boolean isHashSizeOver() {
double size = hash.hashTableCount / hash.capacity;
if (size > 0.5) {
return true;
}
return false;
}
/**
* rehashing
* @return
*/
private void rehashing() {
Node[] tmpTable = hash.table;
hash.capacity = hash.capacity *2;
Node[] newNode = new Node[hash.capacity];
for(int i =0; i< tmpTable.length; i++) {
if (tmpTable[i].usaged == true) {
newNode[i] .key = tmpTable[i].key;
newNode[i] .value = tmpTable[i].value;
newNode[i] .usaged = tmpTable[i].usaged;
}
}
hash.table = newNode;
}
}'Algorithms > structure' 카테고리의 다른 글
| 8. Dynamic Programming(동적 계획법) (0) | 2023.04.18 |
|---|---|
| 7. Priority Queue(우선순위 큐) (0) | 2023.04.18 |
| 5. Tree(트리) (0) | 2023.04.17 |
| 4. Queue(큐) (0) | 2023.04.17 |
| 3. Stack(스택) (0) | 2023.04.17 |
Hash(해시)
정의
- 인덱스를 사용하는 알고리즘으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수이다
- 데이터를 입력받고 완전히 다른 모습의 데이터로 바꾸어 놓는 작업
- 잘게 부수고 다시 뭉치는 것
- 대용량의 데이터를 검색할 때 주로 사용
- 효율적인 탐색 알고리즘을 위한 자료구조로써 Key를 Value에 대응시킨다.
사전구조 개념
- 사전구조는 map이나 table로 불리고 key와 value 두 가지 종류의 필드를 가진다.
- 데이터에 접근하고 삭제할 때 탐색할 key값만 알 수 있으면 된다.
해시의 사용용도
- 해시테이블(Hash Table) : 데이터의 해시 값을 테이블 내의 주소로 이용하는 궁극의 탐색 알고리즘이다.
- 암호화 : 해시는 입력받은 데이터를 완전히 새로운 모습의 데이터로 만든다.(ex- SHA:Secure Hash Algorithm)
- 데이터 축약 : 길이가 서로 다른 입력 데이터에 대해 일정한 길이의 출력을 만들 수 있다. 이 특성을 이용하여 데이터를 ’해시’하면 짧은 길이로 축약할 수 있다.
해시 알고리즘의 용어
- Bucket(버킷) : 해시주소 하나에 1개 이상의 데이터가 저장되는 전체 메모리공간
- Slot(슬롯) : 버킷에서 하나의 데이터가 저장되는 메모리 공간
- Collision(충돌) : 서로 다른 데이터인데 같은 해시주소를 갖게되면 충돌이 발생된다.
- Overflow(오버플로) : 충돌을 예방하기위해 해시주소 1개에 여러 개의 슬롯을 만든다. 그러나 충돌이 계속 발생해서 더 이상 데이터를 저장할 슬롯이 없어지는 상황이 발생하면 오버플로가 발생
- Cluster(클러스터) : 해시 테이블 내의 일부 지역들의 주소를 집중적으로 반환하는 결과로 한 곳에 모이는 문제
해시 테이블 (Hash Table)
- 키 값의 연산에 의해 직접 접근이 가능한 구조로써, 데이터를 담을 테이블을 미리 확보한 후 입력 받은 데이터를 해시(데이터를 잘게 부수고 다시 뭉쳐)하여 테이블 내의 주소를 계산하고 이 주소를 데이터에 담는 것이다.
- 해시테이블은 데이터가 입력되지 않은 공간이 많아야 제 성능을 유지할 수 있다.
해시 함수(Hash function)
- Devision Method(나눗셈법) : 입력 값을 테이블의 크기로 나누고 나머지를 테이블 주소로 사용
- 주소 = 입력 값 % 테이블 크기
- 입력 값이 테이블 크기의 배수 또는 약수인 경우 0을 반환
- 그렇지 않는 경우 n-1을 반환
- 서로 다른 입력 값에 대해 동일한 해시 값, 즉 해시 테이블 내의 동일한 주소를 반환할 가능성이 높음(이것을 충돌(Collision)이라고 함)
- Digits Folding(자릿수 접기) : Collision or Cluster를 줄일 수 있는 알고리즘으로 일정크기 이하의 수로 만드는 방법이다.
- 10진수의 경우 0~9까지 값을 값을 가지므로 한 자리수 접기는 최대 63개 두 자리수 접기는 306까지의 해시 값을 얻을 수 있다.
- Digits Folding은 문자열을 키로 사용하는 해시 테이블에 잘 어울림.
int Digit_Folding_Hash(char* key, int length, int tableSize) {
int i = 0;
int hashValue = 0;
for (i = 0; i<length; i++) {
hashValue += key[i];
}
return hashValue % tableSize;- 문자열 키를 Digits Folding 알고리즘을 통해 키를 만들어내는 코드
- 문자열의 최대길이가 10자리면 해시함수는 10 * 127 1270이므로 1271 사이의 주소는 활용되지 않는다. ASCII로 10자리를 만들었을 때 조합할 수 있는 경우의 수가 127^10 가지나 됨
- 테이블 크기를 2진수로 표현하고 해시 값을 3비트씩 밀어올린 후 ASCII코드 번호를 더하면 해시테이블의 폐가 문제를 해결할 수 있다.
int Digit_Folding_Hash(char* key, int length, int tableSize) {
int i = 0;
int hashValue = 0;
for (i = 0; i<length; i++) {
hashValue = (hashValue << 3) + key[i];
}
return hashValue % tableSize;
}
ex) 7자리의 숫자 819335각 한 자릿수를 더한다
8+1+9+3+3+5 = 31
새로운 값 31이 나온다.
819335는 31로 일정 크기 이하의 수가 나왔다.두 자리씩 더할 경우
81 + 93 + 35 = 148
새로운 값 148이 나옴.
- 해시 함수의 한계
- 해시 함수가 서로 다른 입력 값에 대해 동일한 해시 테이블 주소를 반환하는 것을 ‘Collision’ 이라고 한다.
해싱 (Hashing)
- 해시 테이블을 이용한 탐색 이라고하며, 키 값에 직접 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 접근하는 자료구조. 해시 테이블(Hash Table) 은 키 값의 연산에 의한 직접 접근이 가능한 구조로 해시 테이블(Hash Table)을 이용한 탐색을 해싱(Hashin) 이라고 한다.
- 어떤항목의 탐색 키만을 가지고 바로 항목이 저장되어 있는 배열의 인덱스를 결정하는 기법.
해싱의 구조
해싱은 자료를 저장하는데 배열을 사용한다. 원하는 항목이 저장된 위치를 알고 있다면 빠르게 삽입하거나 꺼낼 수 있다.
- 해시함수(Hash Function) : 탐색 키를 입력받아 해시 주소(Hash Address) 를 생성하고 해시 주소가 배열로 구현된 해시 테이블(Hash Table) 의 인덱스가 된다.

- 해시 테이블 K를 받아서 해시 함수 h()로 연산한 결과인 해시 주소 h(k)를 인덱스로 사용하여 해시 테이블에 있는 항목에 접근한다.
- 해시테이블 ht는 M개의 버켓(bucket) 으로 이루어지는 테이블로써 ht[0], ht[1]… ht[M-1]의 원소를 가진다.

- 버켓은 s개의 슬롯(slot) 을 가질 수 있으며, 하나의 슬롯에는 하나의 항목이 저장된다. 하나의 버켓에 여러 개의 슬롯을 두는 이유는 서로 다른 두 개의 키가 해시 함수에 의해 동일한 주소로 변환될 수 있으므로 여러 개의 항목을 동일한 버켓에 저장하기 위해서이지만, 대부분의 경우 하나의 버켓에 하나의 슬롯을 가진다.
- 해시테이블에 존재하는 버켓의 수가 M이므로 해시 함수 h()는 모든 k에 대해 0 ≤ h(k) ≤ M − 1 의 범위 값을 제공해야한다. 대부분의 경우 해시 테이블의 버켓 수는 키가 가질 수 있는 모든 경우의 수보다 매우 작으므로 여러 개의 서로 다른 탐색 키가 해시 함수에 의해 같은 해시 구조로 사상(Mapping)되는 경우가 자주 발생한다.
- 서로다른 두 개의 탐색 키 K1와 K2에 대하여 h(k1) = h(k2)인 경우를 충돌(Collision) 이라고 한며, 이러한 키 k1, k2를 동의어(synonym) 라 한다.
- 만약 충돌이 발생하면 같은 버켓에 있는 다른 슬롯에 항목을 저장하게 된다.
- 충돌이 자주 일어나면 버켓 내부에서 순차탐색 시간이 길어져 탐색 성능이 저하될 수 있으므로 해시 함수를 수정하거나 해시 테이블의 크기를 적절하게 조절해야한다.
- 충돌이 버켓에 할당된 슬롯 수보다 많이 발생하게 되면 버켓에 더 이상 항목을 저장할 수 없게 되는 오버플로(overflow)가 발생한다. 만약 버켓당 슬롯의 수가 하나(s==1)이면 충돌이 곧 오버플로를 의미한다.
- 오버플로가 발생하면 더 이상 항목을 저장할 수 없으므로 오버플로를 해결하기 위한 방법이 반드시 필요.
해시 알고리즘에서 발생되는 문제들
- 테이블 해시주소의 중복
- 버킷 용량
- 오버플로 해결
- 개방주소법(Open Address) : 해시 함수에 의해 얻어진 주소가 아니더라도 다른 주소를 사용할 수 있도록 허용하는 충돌해결 알고리즘
- 선형조사방법(Linear Proving Method) : 현재 만들어진 해시 주소로 데이터를 넣으려는데 이미 꽉 채워져 있으면 바로 옆자리를 확인하고 옆자리도 채워져 있다면 다시 옆자리로 이동하며 작업을 반복하는 알고리즘
- 구현방법간단, 성능도 soso
- 같은 해시주소를 사용해서 충돌이 발생할 때마다 원래의 해시주소 근처의 주소에 데이터가 집중되는 현상 발생
- 클러스터링(솔림현상)이 발생
- 제곱탐사(Quadratic Probing) : 선형 탐사는 다음 주소를 찾기 위해 고정폭만큼 이동하지만 제곱탐사는 이동폭이 제곱수로 늘어는 것.
- 선형조사방법(Linear Proving Method) : 현재 만들어진 해시 주소로 데이터를 넣으려는데 이미 꽉 채워져 있으면 바로 옆자리를 확인하고 옆자리도 채워져 있다면 다시 옆자리로 이동하며 작업을 반복하는 알고리즘
- 이중해싱(Double Hashing) : 첫 번째 해시함수에서 충돌이 발생할 경우 이동폭을 더하여 다른 해시 함수를 이용하는 것 (테이블의 끝을 만나면 처음부터 다시 탐색)
- 폐쇄주소법(Closed Address) :
- 분리연결법(eperate Chaining) : 연결리스트(Linked List) : 연결리스트를 사용하여 오버플로가 발생하더라도 다른 해시 주소로 이동하지 않고 해당 주소안에 새로운 노드를 생성하여 연결한다. 해시주소는 바뀌지 않는 장점이 있지만 클러스터링이 발생하면 연결리스트 내부에서 검색 작업이 발생한다.
- 리해싱(Rehashing) : 해시 테이블의 크기를 늘리고, 늘어난 해시 테이블의 크기에 맞추어 테이블 내의 모든 데이터를 다시 해싱하는 것
- 개방주소법(Open Address) : 해시 함수에 의해 얻어진 주소가 아니더라도 다른 주소를 사용할 수 있도록 허용하는 충돌해결 알고리즘
해시 알고리즘의 효율성은 해시 함수가 얼마나 복잡한지에 따라 달라진다.
또한 해시 함수 역시 해시 주소를 어떻게 결정할 것인지 또는 Key의 패턴이 어떤지에 따라 달라진다.
충돌 해결하기
- 개방 해싱(Open Hashing) : 해시 테이블의 바깥에 새로운 공간을 할당하여 문제를 수습
- 폐쇄 해싱(Closed Hashing) : 처음에 주어진 해시 테이블 공간에서 문제를 해결
- 체이닝(Chaining) : 해시 함수가 서로 다른 키에 대해 같은 주소값을 반환해서 충돌이 발생하면 각 데이터를 해당 주소에 있는 연결 리스트에 삽입하여 문제를 해결하는 기법
- 체이닝 가반의 해시 테이블은 데이터 대신 연결리스트에 대한 포인터를 관리
- 삽입연산은 충돌이 앞으로 발생할 것을 고려하여 설계
- 삭제, 탐색 연산은 이미 충돌이 발생했을 것을 고려하여 설계
- 체이닝은 오픈 해싱 기법인 동시에 폐쇄 주소법 알고리즘이기도 한다.
체이닝의 탐색순서
- 찾고자하는 목표값을 해싱하여 연결 리스트가 저장되어 있는 주소를 찾음
- 이 주소를 이용하여 해시 테이블에 저장되어 있는 연결리스트에 대한 포인터를 생성
- 연결 리스트 앞에서부터 뒤까지 차례로 이동하며 목표 값이 저장되어 있는지 비교
- 목표값과 연결 리스트 내의 노드 값이 일치하면 해당 노드주소 반환
체이닝의 문제점 및 해결 방법
문제점
- 체이닝은 원하는 데이터를 찾기 위해서 순차탐색을 해야하는 연결리스트의 단점을 가지고 있다.
해결방법
- 레드 블랙 트리 또는 이진탐색 트리를 이용하면 문제를 해결 할 수 있다.
Key-Address 검색 알고리즘
- 인덱스만으로 원하는 데이터를 검색하는 알고리즘이다.
- 비유 : 아파트 우편함 동 호수에 내용물이 담겨있는 것처 해당 key에 데이터가 담겨있는 것을 말함
- O(1) 의 성능을 낸다.
void keyAddress() {
int i = 0;
for (i = 0; i<5; i++) {
student->name ='A'+i;
student->number = 1000+i;
printf("%학번 : %d 이름 : %c\n", student->number, student->name);
}
}위 코드처럼 배열의 인덱스만 알면 비교나 검색할 필요가 없이 해당 데이터에 학번 이름을 출력할 수 있다. 그러나 메모리의 효율성은 떨어진다. 전체 데이터의 크기는 10 바이트라면 저장된 데이터 크미는 5바이트 밖에 사용하지 않았기 때문이다.
Key-Mapping 검색 알고리즘
- Key-Address의 단점을 해결해주는 알고리즘으로 찾고자 하는 데이터를 나눈 나머지 값을 구하는 기능
- 문제점 : 데이터가 중복될 수 있다.
void MakeKeyMapping() {
int i=0, num, idx;
srand((unsigned)time(NULL));
while(i < 50) {
num = rand() % 100;
Buf[num] = num % 50;
idx = num % 50;
Hit[idx].key = idx;
Hit[idx].counter++;
i++;
}
}추상자료형
- 새로운 항목을 사입(add)
- 탐색 키에 관련된 항목을 삭제(delete)
- 탐색 키에 관련된 값을 탐색(search)
- 객체 : 일련의 (key, value) 쌍의 집합
- 연산
- add(key, value) : (key, value)를 사전에 추가
- delete(key) : key에 해당되는 (key, value)를 찾아서 삭제하고 관련된 value는 반환한다. 탐색에 실패하면 null을 반환
- search(key) : key에 해당되는 value를 찾아서 반환. 만약 탐색이 실패하면 null을 반환
ex)
Hash.h
#ifndef HASH_H
#define HASH_H
#include <Stdio.h>
#include <stdlib.h>
#include <memory.h>
#include <string.h>
typedef char* KeyType;
typedef char* ValueType;
typedef struct _tagNode {
KeyType key;
ValueType value;
struct _tagNode *next;
}Node;
typedef Node* List;
typedef struct _HashTable {
int tableSize;
List* table;
}_HashTable;
typedef struct tagHashTable {
int tableSize;
Node* table;
}HashTable;
HashTable* SHT_createHashTable(int tableSize);
void SHT_Put(HashTable* HT, KeyType key, ValueType value);
ValueType SHT_Get(HashTable* HT, KeyType key);
void SHT_DestoryHashTable(HashTable* HT);
int SHT_Hash(int input, int tblSize);
int Digit_Folding_Hash(char* key, int length, int tableSize);
HashTable* CHT_CreateHashTable(int tableSize);
void CHT_DestoryHashTable(_HashTable* HT);
Node* CHT_CreateNode(KeyType key, ValueType value);
void CHT_DestoryList(List List);
void CHT_DestoryNode(Node* node);
void CHT_Set(_HashTable* HT, KeyType key, ValueType value);
int CHT_Hash(KeyType key ,int length, int tableSize);
ValueType CHT_Get(_HashTable* HT, KeyType key);
#endif //HASH_H나눗셈법을 이용한 hashtable
SimpleHashTable.c
#include "Hash.h"
HashTable* SHT_createHashTable(int tableSize) {
HashTable* HT = (HashTable*)malloc(sizeof(HashTable));
HT->table = (Node*)malloc(sizeof(Node)* tableSize);
HT->tableSize = tableSize;
return HT;
}
void SHT_Put(HashTable* HT, KeyType key, ValueType value) {
int adr = SHT_Hash(key, HT->tableSize);
HT->table[adr].key = key;
HT->table[adr].value = value;
}
ValueType SHT_Get(HashTable* HT, KeyType key) {
int adr = SHT_Hash(key, HT->tableSize);
return HT->table[adr].value;
}
void SHT_DestoryHashTable(HashTable* HT) {
free(HT->table);
free(HT);
}
int SHT_Hash(int input, int tblSize) {
return input % tblSize;
}체이닝을 이용한 해시
#include "Hash.h"
int CHT_Hash(KeyType key ,int length, int tableSize) {
int hashKey = 0;
int i = 0 ;
for (i = 0; i<length; i++) {
hashKey = (hashKey << 3) + key[i];
}
return hashKey % tableSize;
}
void CHT_Set(_HashTable* HT, KeyType key, ValueType value) {
int idx = CHT_Hash(key, strlen(key), HT->tableSize);
Node* newNode = CHT_CreateNode(key,value);
if (HT->table[idx] == NULL) {
HT->table[idx] = newNode;
printf("put : key(%s), idx(%d)\n", key,idx);
} else {
List list = HT->table[idx];
newNode->next = list;
HT->table[idx] = newNode;
printf("Collision occured : key(%s), idx(%d)\n", key,idx);
}
}
ValueType CHT_Get(_HashTable* HT, KeyType key) {
int idx = CHT_Hash(key, strlen(key), HT->tableSize);
List list = HT->table[idx];
List Target = NULL;
if (list == NULL) {
return NULL;
}
while(1) {
if (strcmp(list->key, key) == 0) {
Target = list;
break;
}
if (list->next == NULL) {
break;
}
else {
list = list->next;
}
}
return Target->value;
}
HashTable* CHT_CreateHashTable(int tableSize) {
_HashTable* hashTable = (_HashTable*)malloc((sizeof(_HashTable)));
hashTable->table = (List*)malloc((sizeof(List) * tableSize));
memset(hashTable->table,0, sizeof(List) *tableSize);
hashTable->tableSize = tableSize;
return hashTable;
}
Node* CHT_CreateNode(KeyType key, ValueType value) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->value = value;
newNode->key = key;
newNode->next = NULL;
return newNode;
}
void CHT_DestoryHashTable(_HashTable* HT) {
int i =0;
for (i=0;i<HT->tableSize; i++) {
List L = HT->table[i];
CHT_DestoryList(L);
}
free(HT->table);
free(HT);
}
void CHT_DestoryNode(Node* node) {
free(node->key);
free(node->value);
free(node);
}
void CHT_DestoryList(List list) {
if (list == NULL) {
return;
}
if (list->next != NULL) {
CHT_DestoryList(list->next);
}
CHT_DestoryNode(list);
}선형탐색법 사용, 이중 해싱, 리해싱.
public class HashTable implements Hash {
private TagHashTable hash;
public HashTable() {
this.hash = new TagHashTable();
}
public HashTable(int capacity) {
this.hash = new TagHashTable(capacity);
}
private class TagHashTable {
Node[] table = null;
private int capacity = 0;
private int hashTableCount = 0;
private static final int DEFAULT_CAPACITY = 100;
public TagHashTable(int capacity) {
this.capacity = capacity;
this.hashTableCount = 0;
this.table = new Node[this.capacity];
}
public TagHashTable() {
this.capacity = DEFAULT_CAPACITY;
this.hashTableCount = 0;
this.table = new Node[this.capacity];
}
}
private class Node {
private int key;
private Object value;
private boolean usaged;
public Node() {
this.key = 0;
this.value = null;
this.usaged = false;
}
public Node(int key, Object value) {
this.key = key;
this.value = value;
this.usaged = false;
}
}
/**
* 1. 해시테이블 크기 계산
* 2. 해시테이블 크기가 50%가 넘으면 리해싱
* 3. 중복키 확인
* 4. 해시 적용
*/
@Override
public void put(String key, Object value) {
if (isHashSizeOver()) {
rehashing();
}
int key1 = hash(key, key.length(), hash.capacity);
int key2 = hash2(key, key.length(), hash.capacity);
while (hash.table[key1] != null && hash.table[key1].usaged != false && hash.table[key1].key != key1) {
key1 = (key1 + key2) % hash.capacity;
}
Node newNode = new Node();
newNode.key = key1;
newNode.value = value;
newNode.usaged = true;
hash.table[key1] = newNode;
hash.hashTableCount++;
}
@Override
public Object get(String key) {
int key1 = hash(key, key.length(), hash.capacity);
int key2 = hash(key, key.length(), hash.capacity);
while(hash.table[key1] != null && hash.table[key1].usaged != false && hash.table[key1].key != key1) {
key1 = (key1 + key2) % hash.capacity;
}
return hash.table[key1].value;
}
@Override
public void remove(String key) {
}
private int hash(String key, int length, int capacity) {
int hashKey = 0;
for (int i =0; i<length; i++) {
hashKey = (hashKey << 3) + key.charAt(i);
}
return hashKey % capacity;
}
private int hash2(String key, int length, int capacity) {
int hashKey = 0;
for (int i =0; i<length; i++) {
hashKey = (hashKey << 3) + key.charAt(i);
}
return (hashKey % (capacity -3) ) + 1;
}
private boolean isHashSizeOver() {
double size = hash.hashTableCount / hash.capacity;
if (size > 0.5) {
return true;
}
return false;
}
/**
* rehashing
* @return
*/
private void rehashing() {
Node[] tmpTable = hash.table;
hash.capacity = hash.capacity *2;
Node[] newNode = new Node[hash.capacity];
for(int i =0; i< tmpTable.length; i++) {
if (tmpTable[i].usaged == true) {
newNode[i] .key = tmpTable[i].key;
newNode[i] .value = tmpTable[i].value;
newNode[i] .usaged = tmpTable[i].usaged;
}
}
hash.table = newNode;
}
}'Algorithms > structure' 카테고리의 다른 글
| 8. Dynamic Programming(동적 계획법) (0) | 2023.04.18 |
|---|---|
| 7. Priority Queue(우선순위 큐) (0) | 2023.04.18 |
| 5. Tree(트리) (0) | 2023.04.17 |
| 4. Queue(큐) (0) | 2023.04.17 |
| 3. Stack(스택) (0) | 2023.04.17 |