반응형
구간합
구간 합은 합 배열을 이용해서 시간 복잡도를 줄이기 위해 사용하는 알고리즘
합 배열 S의 정의
- A[0]부터 A[i]까지의 합
S[i] = A[0] + A[1] + A[2] + … + A[i-1] + A[i];
합 배열은 기존의 배열을 전 처리한 배열로써 이런 식으로 미리 구해 놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(n) 에서 O(1)로 감소
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 배열A | 15 | 13 | 10 | 7 | 3 | 12 |
| 합배열 S | 15 | 28 | 38 | 45 | 48 | 60 |
합 배열 S를 만드는 공식
S[i] = S[i-1] + A[i]
구간 합을 구하는 공식
S[j] - S[i-1] //i에서 j까지의 구간 합
- 구간 합을 예제
import java.util.Scanner;
public class 구간합구하기4_11659 {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int N = scan.nextInt();
int M = scan.nextInt();
int[] S = new int[N + 1];
S[1] = S[1] + scan.nextInt();
for (int i = 2; i <= N; i++) {
S[i] = S[i-1] + scan.nextInt(); //합배열 S를 만드는 공식
}
for (int seq = 0; seq < M; seq++) {
int i = scan.nextInt();
int j = scan.nextInt();
int sum = S[j] - S[i-1]; //구간 합을 구하는 공식
System.out.println(sum);
}
}
}2차원 구간 합 배열 D[X][Y] 정의
D[x][y] = 원본 배열의 (0,0)부터 (x,y)까지 사각형 영역 안있는 수의 합
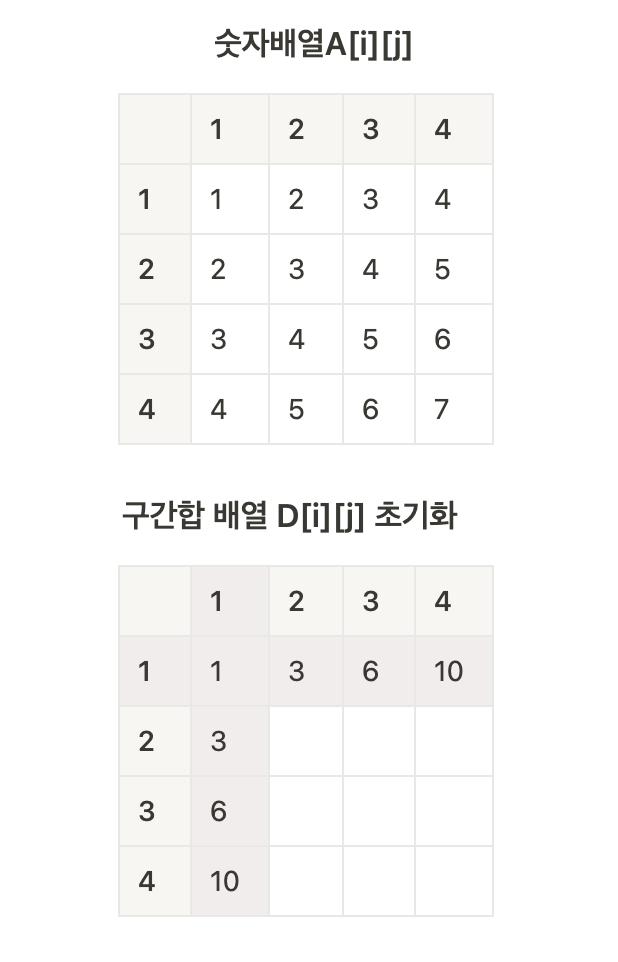
- 가로 구간 합 배열
D[1][j] = D[1][j-1] + A[1][j]
- 세로 구간 합 배열
D[i][1] = D[i-1][1] + A[i][1]
D[i][j]의 값을 채우는 구간 합 공식
D[i][j] = D[i][j-1] + A[i-1][j] + A[i-1][j-1] + A[i][j]
public class PrefixSum {
public static void main(String[] args) {
int[][] a = new int[][] {{0,1,2,3,4}, {0,2,3,4,5}, {0,3,4,5,6}, {0,4,5,6,7}};
int[][] sum = new int[a.length+1][a.length+1];
for (int i = 0 ; i < a.length; i++) {
for (int j = 1; j < a[i].length; j++) {
sum[i+1][j] = sum[i+1][j-1] + sum[(i+1)-1][j] - sum[(i+1)-1][j-1] + a[i][j];
}
}
int x1 = 2;
int y1 = 2;
int x2 = 3;
int y2 = 4;
int result = sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1];
System.out.println(result);
}
}반응형
'Algorithms > structure' 카테고리의 다른 글
| 12. Graph(그래프) (0) | 2023.04.18 |
|---|---|
| 11. Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.18 |
| 10. DeviedAndConquer(분할정복) (0) | 2023.04.18 |
| 9. Sort(정렬) (0) | 2023.04.18 |
| 8. Dynamic Programming(동적 계획법) (0) | 2023.04.18 |